Como estuvimos hablando hoy en la meet, llegó el tan ansiado día 😂 en el que vamos a aprender a salvar las indeterminaciones de los límites
Antes vamos a escribir las conclusiones que llegamos a partir de las tablas de valores (están en la carpeta de clases virtuales) del desafío de la clase anterior:
Empecemos...
Indeterminación del tipo 0/0.
Miren el siguiente ejemplo:
Como es una indeterminación del tipo 0/0, no nos va a servir que apliquemos las propiedades para intentar salvarlo, entonces ¿qué hacemos?
Como pueden ver, el 2 (número al que tiende el límite) es raíz de ambos polinomios (tanto como para el que está en el numerador como para el que está en el denominador) ya que cuando reemplazamos el 2 en las x, los mismos nos dan 0.
Entonces, para simplificar las cosas y ayudarnos a salir de este lío, lo que vamos a hacer es factorizar los polinomios. Si se acuerdan como, buenísimos, y sino, ahora les refresco la mente...
Hay muchas maneras de factorizar un polinomio.
Siempre que el polinomio esté expresado de forma polinómica, podemos cambiar la forma en la que está escrito y podemos expresarlo en función de sus raíces.
¿Cómo sería eso? pues, así:
Suponiendo que el grado (número del exponente mas grande) del polinomio es 2, la forma polinómica sería la siguiente: 
y si consideramos que X₁ y X₂ son las raíces del mismo, la forma factorizada queda así:
Mientras mayor sea el grado del polinomio, más raíces puede tener el mismo.
Hay otras formas que son útiles recordarlas como la diferencia de cuadrados o también el desarrollo del cuadrado del binomio.
Les muestro igualdades a tener en cuenta:
Ahora bien, vamos a hacer un ejemplo de una indeterminación del tipo 0/0 y cómo resolver la misma.
Para resolver este problema, mas precisamente para factorizar el polinomio del numerador, debemos aplicar la regla de Ruffini. Si no se la acuerdan, no importa, se las explico.
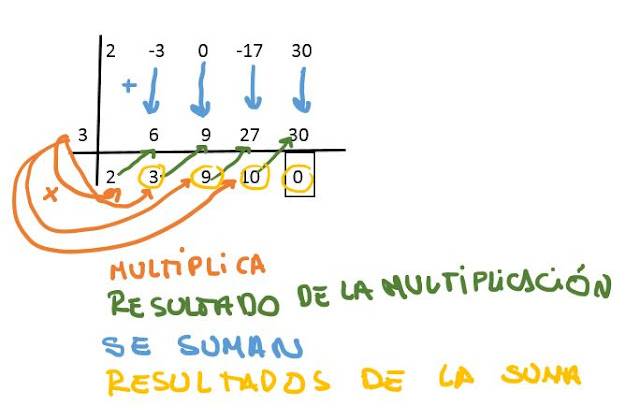
Paso 1: Armamos el cuadrito
En el cuadro, vamos a escribir los coeficientes, de forma completa y ordenada, que multiplican al polinomio (sólo los números que acompañan a las x) en la parte de arriba a la derecha. Luego en la parte de abajo a la izquierda, ponemos la raíz del polinomio, que de ventaja sabemos que es el número al que tiende el límite, ya que cuando lo reemplazamos nos dió 0 y por último bajamos el primer coeficiente en la parte derecha.
Y el cuadrito quedaría una cosa así:
Fíjense que puse un 0 en donde debería ir el coeficiente de la x². Eso lo vamos a hacer siempre que el coeficiente sea 0 (nos damos cuenta porque ese término no está).
Paso 2: Operamos
Una vez que ya tenemos el cuadro, realizamos las operaciones correspondientes. Primero, el primer coeficiente se multiplica con la raíz, y al valor que nos de le sumamos el segundo coeficiente y así sucesivamente.
Paso 3: Reescribir el polinomio
Ahora bien, tenemos el resultado de la división (porque eso es lo que hace Ruffini) a partir de la raiz. Entonces podemos reescribir el polinomio como la multiplicación entre esa raiz y el resultado que nos dió.
Para reescribir el resultado obtenido, recuerden que Ruffini "baja" un grado del polinomio, lo que significa que si era grado 4, ahora el resultado, es grado 3.
Quedaría escrito de la siguiente forma:
Y ahora solo queda reemplazar el polinomio original por éste que es el mismo pero, escrito de otra forma.
Entonces, como los polinomios del numerador se están multiplicando, podemos simplificar con el x-3 del denominador y nos queda:
Y entonces nos permite resolver el límite sin ningún problema.
Recuerden que tienen más ejemplos en la meet de hoy (grabada en la carpeta de clases virtuales) , y además también cuentan con mi canal de YouTube donde explico todos los casos de factoreo de polinomios.
Para el próximo Miércoles, tengan resueltas las siguientes actividades.
Cualquier consulta no duden en escribirme.
❤ ¡Los quiero! ❤
Prof. Agustina (agustina.innocenti@bue.edu.ar)