FÍSICA 4A Y 4B

 Hola a todos!!!

Como se habrán dado cuenta (porque les mandé una notificación anoche) cancelé la meet de hoy. Lo hice porque me parece mejor que primero lean y piensen en ciertos conceptos antes de que se los explique yo de cero.

Último tema del año! A ponerle pilas!

MOVIMIENTO PARABÓLICO O TIRO OBLICUO:

El movimiento parabólico de caída libre o MPCL, es un movimiento cuya trayectoria es una curva llamada parábola (lo vimos en 3ro cuando vimos función cuadrática, su gráfico es una parábola), en el cual el cuerpo se mueve únicamente bajo la influencia de la gravedad una vez que es liberado (en el vacío, sin aire).

Si un cuerpo se tira en forma inclinada o se tira en forma horizontal y se mueve cerca a la tierra despreciando la resistencia del aire, hace un movimiento parabólico de caída libre, influenciado por la aceleración de la gravedad.

El movimiento parabólico de caída libre es un movimiento que está formado por 2 movimientos que se realizan al mismo tiempo y de forma independiente. En el eje horizontal (x) se desarrolla un movimiento rectilíneo uniforme o MRU; mientras que en el eje vertical (y) se desarrolla un movimiento vertical de caída libre o MVCL.

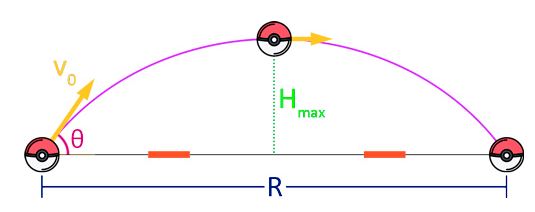
Tranquilos, me imagino que vieron esta imagen y quisieron cerrar todo, pero a no desesperar, vamos de a poco, paso a paso.

Les va a pasar que en la mayoría de los ejercicios van a tener que descomponer el movimiento parabólico en estos 2 movimientos para poder hallar las respuestas. 

Y para esto tenemos que refrescar como descomponer una fuerza en sus componentes del eje y y del eje x (lo vimos a principio de año).

Ahora si, habiendo refrescado esto, veamos las fórmulas del movimiento parabólico de caída libre.

Si se fijan bien, la velocidad, en este tipo de movimiento está compuesto por un movimiento en vertical y otro en horizontal, por lo que va a tener distintas velocidades dependiendo cual eje analizo.

En el eje x describe un movimiento uniforme , entonces la fórmula que vamos a utilizar es:

Para describir el movimiento en el eje y, lo tenemos que pensar como un tiro vertical o caída libre, por ende vamos a usar las fórmulas que ya conocemos pero con determinadas diferencias:

Vamos a usar cuatro fórmulas nuevas que nos van a sacar las papas del fuego y nos van a ahorrar mucho tiempo:

Antes de empezar a hacer los ejercicios piensen que el truco consiste en analizar el movimiento en dos partes: uno en el eje x (MRU) y el otro en el eje y (TV y CL)

EJEMPLO

Desde la terraza de un edificio de 4,9 metros de altura se tira horizontalmente una pelota de básquet y cae al suelo en un punto situado a 7 metros del borde del edificio. Hallar la velocidad de la pelota en el instante en que fue lanzada. 

Sabemos que lo mejor a la hora de intentar resolver un ejercicio es hacer un esquema del mismo:

Acordémonos también que el movimiento parabólico de caída libre es un movimiento formado por un MVCL en el eje y y un MRU en el eje x. Antes de usar alguna de las fórmulas, tenemos que verificar ls unidades y en este ejercicio,  todos los valores se encuentran en el  mismo sistema  de unidades.

En el eje y, podemos usar la siguiente fórmula, teniendo en cuenta que la velocidad inicial en el eje y es cero, ya que la pelota se tira horizontalmente, es como si la empujaras y termina cayendo.

Y para el eje x podemos usar:

Por lo que podemos decir que la velocidad de la pelota en el instante en el que fue lanzada es 7 m/s.

Miren el siguiente video para aclarar mas dudas.

Para la clase que viene tienen que tener marcadas dudas puntuales acerca de este nuevo movimiento. Quédense tranquilos que vamos a hacer varios ejemplos más antes de trabajar con la guía de actividades.

¡Buen Martes para todos!

Prof. Agustina (agustina.innocenti@bue.edu.ar)