Hola a todos!
Ya vimos una introducción a función logarítmica. Ahora vamos a ver más en detalle como funcionan cada uno de sus elementos y como realizar una análisis más completo de la misma.
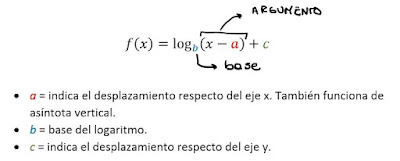
Partiendo de como se escribe la fórmula general de la función, vamos a nombrar cada una de sus partes y como juegan en este partido:
Ahora analicemos la función:
1) Dominio:
Para averiguar el dominio, sea cual sea la función, tenemos que encontrar las restricciones del mismo (los valores que no puede tomar x) y para eso tenemos que pensar que no se puede hacer.
En el caso de una función logarítmica, el argumento NUNCA puede ser negativo, y tampoco puede ser 0. Por eso, la operación que vamos a realizar es:
2) Imagen:
Lo bueno de la imagen de las funciones logarítmicas, es siempre la misma, y esta es:
3) Intersecciones con los ejes:
- Intersección con el eje x (raíz): "y=0"
Para hallar la raíz siempre hay que igualar la función a 0 y despejar x.
- Intersección con el eje y (ordenada al origen): "x=0"
4) Asíntotas:
Para la asíntota no hay que hacer ningún cálculo. Simplemente es reconocer que es el numero que está sumando a la x en el argumento.
Sólo tiene asíntota vertical.
5) Conjuntos de positividad y de negatividad:
Siempre teniendo en cuenta que los intervalos se escriben en función del eje x. En el caso de tener ambos conjuntos, los intervalos van a estar marcados por la raíz.
6) Intervalos de crecimiento y de decrecimiento:
La función logarítmica es creciente o decreciente en todo su dominio. Por lo tanto solo tiene uno de los dos intervalos, nunca va a tener ambos.
Veamos un ejemplo: